
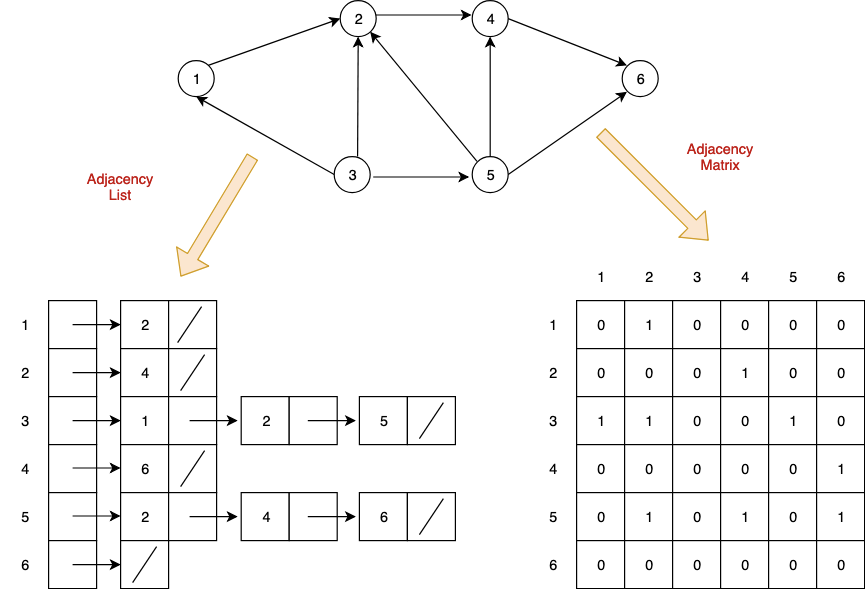
If we define the polynomials \(s_1(x,y) = x+y\) and \(s_2(x,y) = xy\) then G(t) = t^2 - (\lambda_1+\lambda_2) t + \lambda_1\lambda_2įrom which we see that the coefficient of \(t\) and the constant term of \(g(t)\) are polynomial expressions in the roots \(\lambda_1\) and \(\lambda_2\). A finite graph can be represented in the form of a square matrix on a computer, where the boolean value of the matrix indicates if there is a direct path between two vertices. For example, expanding the polynomial \(g(t) = (t-\lambda_1)(t-\lambda_2)\) we obtain An adjacency matrix is a way of representing a graph as a matrix of booleans (0's and 1's). Recall that the eigenvalues of a matrix are the roots of its characteristic polynomial and the coefficients of a polynomial depend in a polynomial way on its roots. The value 1 represents the edge between two vertices.

If the graph has no loops, then the adjacency matrix has 0s in the diagonal positions.

The adjacency matrix is symmetric for an undirected graph. The coefficients and roots of a polynomialĪs mentioned at the beginning of this chapter, the eigenvalues of the adjacency matrix of a graph contain valuable information about the structure of the graph and we will soon see examples of this. Adjacency Matrix is a simple way of representing the graph having n vertices of the square matrix M. Prove that the total number of walks of length \(k\geq 1\) in \(G\) is \(n r^k\). The identity matrix will be denoted by \(\bs\). This approach to graph theory is therefore called spectral graph theory.īefore we begin, we introduce some notation. The edge-adjacency matrix, denoted by eA, of an edge-labeled connected graph G is a square E × E matrix which is determined by the adjacencies of edges 2. In particular, the eigenvalues and eigenvectors of the adjacency matrix can be used to infer properties such as bipartiteness, degree of connectivity, structure of the automorphism group, and many others. In this chapter, we introduce the adjacency matrix of a graph which can be used to obtain structural properties of a graph. 2.3 The characteristic polynomial and spectrum of a graph.2.2 The coefficients and roots of a polynomial.


 0 kommentar(er)
0 kommentar(er)
